A complicated name for an easy way to make better microscopes
Here is a short video lecture that summarizes Fourier ptychography for a general audience:
Here is a series of Fourier Ptychography review articles that we recently published in Microscopy Today:
The Horstmeyer Lab team has created a series of 3 articles to explain Fourier ptychography the non-specialist. Please take a look at the articles linked below to learn more!
Article #1: Introduction to Fourier Ptychography: Part I - Microscopy Today (2022)
Article #2: Fourier Ptychography Part II: Phase Retrieval and High-Resolution Image Formation - Microscopy Today (2022)
Article #3: Applications and Extensions of Fourier Ptychography - Microscopy Today (2022).
This work also made the cover of Microscopy Today!

A Brief Introduction to Fourier Ptychography
Right now, all of the images we take (whether with our cell phone cameras or in a microscope) have several to tens of million pixels in them. This isn’t a coincidence. Ever since the first lens was designed many centuries ago, so was the first aberration, which causes the resulting image to appear blurry. Only within a certain “sweet spot” does an image actually appear sharp and clear. This “sweet spot”, also called the lens field-of-view, limits all of the images we take to only contain megapixels, instead of gigapixels.
Fourier ptychography (with a silent 'p') uses computation to significantly improve upon this sweet spot. First, it captures multiple images using a lens with a very large field-of-view, but which otherwise exhibits poor resolution. Second, it combines the captured images together into a very high resolution reconstruction, using a phase retrieval algorithm. Here's an example reconstruction:

A critical component of our new approach is the use of an LED array, which we use to illuminate our microscope sample from a number of different angles. Each time we turn on a different LED, we capture a unique image. The light from each angled LED effectively shifts new information emerging from the sample into the microscope lens. The sequence of captured images contains enough information to allow us to computationally recover very high resolution sample features (so far, down to approximately 300 nanometers). At the end of the day, we can increase the number of resolvable pixels in an image by a factor of approximately 50-100X, creating some of the first gigapixel images in an imaging system without any moving parts. The technique also increases the microscope working distance and depth-of-field, computationally corrects for system aberrations, and removes the need for oil immersion.
Please see our recent Fourier Ptychography review paper for more information about this powerful technique:
P. Konda et al., "Fourier ptychography: current applications and future promises," Optics Express 2020.
3D Imaging with Fourier Ptychography
We have been developing a new way to capture and reconstruct thick samples in 3D without re-focusing or moving anything. Instead, we simply turn on different LEDs and capture multiple images, just like as outlined above. Then, we use a new algorithm to combine the captured data into a 3D "tomographic" reconstruction. We call our new measurement and reconstruction process "Fourier ptychographic tomography" (FPT, for short). Unlike the related method of diffraction tomography, FPT just measures normal intensity-only images, and does not need a reference beam to measure phase. This allows FPT to measure very small changes in the index of refraction of primarily transparent samples without using any interferometry (i.e., using a phase-stable laser and a reference beam). Please see the following paper for more details about this new 3D imaging technique:
Associated paper: R. Horstmeyer et al., "Diffraction tomography with Fourier ptychography," Optica (2016)
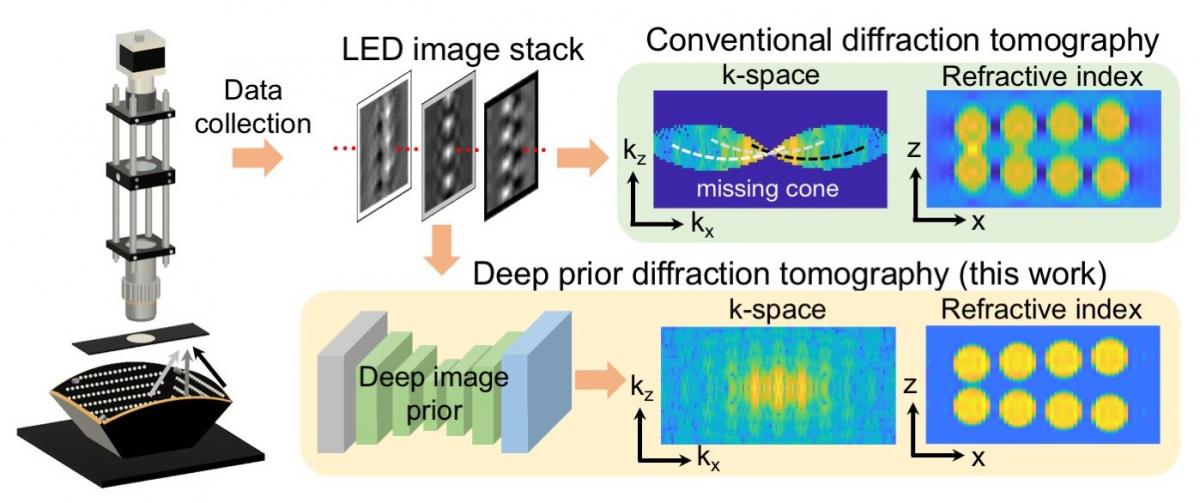
Deep Learning with Fourier Ptychography
As with many imaging modalities, Fourier ptychography can also directly benefit from the recent advent of new deep machine learning tools. One key example is to improve the quality of Fourier ptychography's high-resolution 3D images (via FPT, see above). It is generally challenging for all imaging modalities to fully sample enough data to produce high-quality 3D images without yielding any image artifacts. What's more, to efficiently obtain and process image data, it is better to capture fewer images. Recently, we demonstrated a technique for 3D Fourier ptychography that utilizes an untrained deep convolutional neural network (CNN) to improve the quality of its resulting 3D reconstructions from a relatively small number of images. The technique relies on a recently proposed "Deep Image Prior" technique, which optimizes the weights within a randomly seeded, untrained CNN, as opposed to the 3D reconstruction itself, to obtain a final high-quality result. More information can be found in our recent publication:
Associated paper: K. Zhou and R. Horstmeyer, "Diffraction tomography with a deep image prior," Optics Express 2020.
Project page with data and source code: https://deepimaging.io/projects/deep-prior-diffraction-tomography/